The objectives of this project are various and diversified in different research fields of Mathematical Analysis as Ordinary Differential Equations, Elliptic Partial Differential Equations, Calculus of Variations,
Set-valued Analysis, Non-smooth Analysis, Minimax Problems, Global Optimization of Connected Functionals, Maximum Principles, Variational and Variational-Hemivariational Inequalities, Qualitative Properties of Solutions, Modular Spaces (Orlicz Spaces, as in particular, Sobolev Spaces with Variable Exponent), Discrete and Fractionals Problems, and so on. In this project, however, all previous arguments are linked by a common denominator that we can summarize as “Nonlinear Differential Problems”.
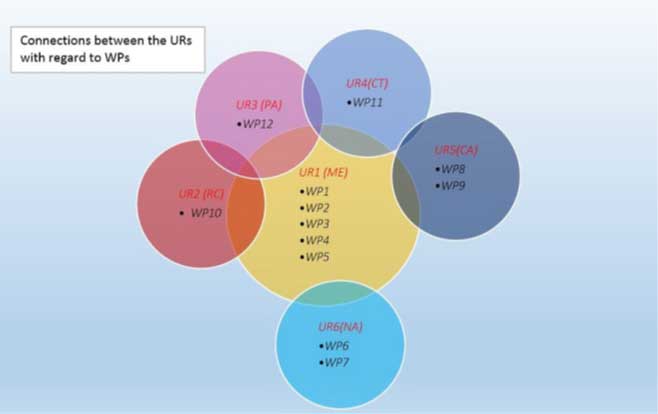
The workplace is divided into 12 work-packages (WP).
WP1: Applications of the critical point theorems to ordinary differential problems (UR1, UR2,UR3 UR4, UR5, CR1, CR3, CR6, CR8, CR12)
WP2: Applications of the critical point theorems to partial differential problems (UR1, UR2, UR3, UR4, UR5, CR5, CR9, CR10, CR11)
WP3: Extension of some results on the existence of a local minimum to non-differentiable functionals (UR1, UR3, CR6, CR9)
WP4: Study of the nature of the solutions of the problem when it is of variational type (UR1.UR2,UR3, CR1,CR13)
WP5: Study of compactness type conditions (UR1, UR2, UR3, UR5, CR11)
WP6: Analysis of several economic and financial equilibrium models by using a variational approach. (UR1, UR6, CR2, CR4)
WP7: Introduction of the nearness condition of Campanato type for set-valued mappings (UR1, UR4,UR6, CR2, CR4, CR7)
WP8: study of non-local problems of both stationary and evolutive type (UR4,UR5,UR6, CR9, CR10, CR11, CR12)
WP9: study of Keller-Segel-type systems (UR1, UR5, CR7, CR12)
WP10: Analysis of non variational problems (UR1, UR2,UR3, CR5, CR6, CR11)
WP11: study of the properties of regularity up to the boundary (of the gradient) of the weak solutions of some nonlinear differential operators (UR4, UR5, CR10, CR11, CR13)
WP12. Variational methods applied to wave propagation phenomena in anisotropic media and in the presence of metamaterials (UR1, UR2, UR3, CR6, CR7)